Rancangan Acak Lengkap Faktorial (RALF)
Laporan Praktikum Rancangan Acak Lengkap Faktorial (RALF)
Nama : Teuku Ariel Alfarisi
No Komputer : 20
Banda Aceh 2024
TINJAUAN PUSTAKA
MENGANALISIS DATA
PADA RANCANGAN ACAK LENGKAP POLA FAKTORIAL
A. Definisi Rancangan Acak Lengkap Faktorial (RALF)
Rancangan Acak Lengkap Pola Faktorial AxB adalah rancangan acak lengkap yang terdiri dari dua peubah bebas (Faktor) dalam klasfikasi silang yaitu faktor A yang terdiri dari a taraf dan faktor B yang terdiri dari b taraf dan kedua faktor tersebut diduga saling berinteraksi. Saling berinteraksi dimasudkan bahwa pengaruh suatu faktor tergantung dari taraf faktor yang lain, dan sebaliknya jika tidak terjadi interaksi berarti berarti pengaruh suatu faktor tetap pada setiap taraf faktor yang lain. Jadi bila tidak terjadi interaksi antar taraf-taraf suatu faktor saling sejajar satu sama lainnya, sebaliknya bila ada interaksi tidak saling sejajar.
B. Pengaturan Unit-Unit Percobaan
Prinsip : Semua unit penelitian (perlakuan dan ulangannya) disebar secara acak disatu tempat dan perlakuan terdiri dari 2 atau lebih dari 2 faktor perlakuan.
Contoh : 2 taraf dosis mikoriza dan 3 taraf dosis rizhobium, dengan 3 ulangan.
Gambar 1. Bagan penelitian untuk RALF dua perlakuan, 2 taraf mikoriza dan 3 taraf rizhobium dengan 3 ulangan.
C. Model Matematika
Hijk = π + Pj + Pk + (Pj x Pk) + eijk
Keterangan :
Hijk = Hasil akibat perlakuan ke-j dan perlakuan ke-k pada ulangan ke-i
Π = Nilai tengah umum
Pj = Pengaruh faktor perlakuan ke-j
Pk = Pengaruh faktor perlakuan ke-k
Pj x Pk = Interaksi perlakuan ke-j dan perlakuan ke-k
Eijk = Eror akibat perlakuan ke-j dan perlakuan ke-k pada ulangan ke-i
I = 1, 2, …., u (u = ulangan)
J = 1, 2, …., p ke-1 (p = perlakuan ke-1)
K = 1, 2,…... p ke-2 (p = perlakuan ke-2)
Keterangan :
Hijk = Hasil akibat perlakuan ke-j dan perlakuan ke-k pada ulangan ke-i
Π = Nilai tengah umum
Pj = Pengaruh faktor perlakuan ke-j
Pk = Pengaruh faktor perlakuan ke-k
Pj x Pk = Interaksi perlakuan ke-j dan perlakuan ke-k
Eijk = Eror akibat perlakuan ke-j dan perlakuan ke-k pada ulangan ke-i
I = 1, 2, …., u (u = ulangan)
J = 1, 2, …., p ke-1 (p = perlakuan ke-1)
K = 1, 2,…... p ke-2 (p = perlakuan ke-2)
Data Rancangan Acak Lengkap Faktorial (RALF) :
Analisis : Rancangan Acak Lengkap Faktorial Pada SPSS
Langkah-langkah penyelesaian RALF (Faktorial) dengan SPSS 16 sebagai berikut:
Langkah 1: Jalankan program SPSS 16
Ketika membuka Program SPSS, ada dua Windows yang muncul yang pertama Untuk Data dan yang kedua yaitu Untuk Output setelah menganalisis.
Tampilan SPSS Bagian Data
Tampilan SPSS Bagian Output
Ada dua tempat yang harus diisi dalam SPSS, yaitu data view (untuk mengisi data yang akan diolah), dan variable view (untuk tempat variable, atau sumber keragaman dalam tabel sidik ragam).
Mengisi Data Pada Data View
Langkah 2 : Mengisi Bagian Kolom Name Seperti di bawah ini

Langkah 3 : Selanjutnya pada “Decimals” disesuaikan berapa banyak decimal yang akan kita gunakan.
Langkah 4 : Setelah bagian Decimals, selanjutnya bagian “Label” buat sesuai dengan Skripsi

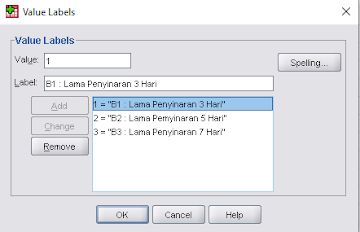
Langkah 5 : Mengisi Bagian “Values” (Bagian Perlakuan A dan Bagian Perlakuan B Serta Ulangan)
Pada Perlakuan A Value diisi dengan A1 Ekstrak 1 ml dan seterusnya Seperti pada gambar
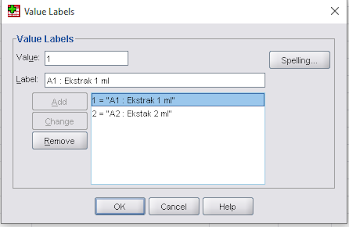

Pada Perlakuan B Value diisi dengan B1 Lama Penyinaran 3 hari dan diikuti seperti gambar
Pada Ulangan Value diisi Dengan 1 Ulangan dan Seterusnya
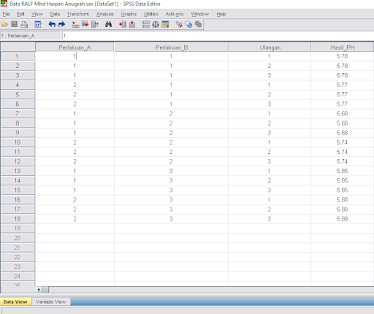
Pada Bagian Label Diklick lalu menjadi data yang seperti dibawah :
Langkah 7 : Menganalisis Data
Klik Bagian Analyze General Linear Model à Univariate
Langkah 8 : Setelah itu muncul seperti di bawah ini Lalu Masukkan Seperti dibawah
Klik hasil Ph Ke Dependent variabel dan Seterusnya
Langkah 9 : Klik Bagian Model kemudian Klik Custom
pada Custom Masukkan Perlakuan A dan B Lalu Ubah ke Main Effect
Langkah 10 : Klik bagian Post Hoc, Post Hoc berfungsi untuk menguji Lanjut dari Hasil Penelitian
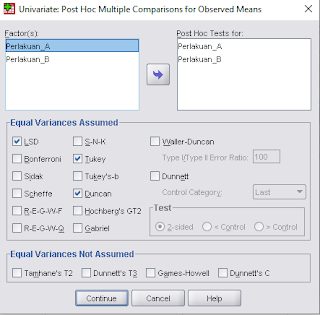
Langkah 11 : Klik bagian Options Masukkan Overal dan Seperti dibawah
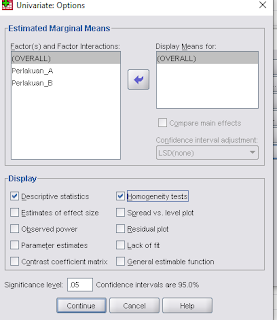
Output Rancangan Acak Lengkap Faktorial (RALF) :











Komentar
Posting Komentar